В ноябре 2014 года я делился своими мыслями по поводу нового алгоритма агрегирования, названного мной «Среднее с динамическими весами». Трудно представить, но с тех пор прошло уже 4.5 года. Еще труднее представить, чтобы с тех пор по данной теме у нас не появилось никаких новостей. И они появились. Поэтому приглашаю вас вернуться к среднему с динамическими весами и посмотреть на этот алгоритм чуть более пристально…

Хороший

Зачем понадобился этот алгоритм? Потому что широко применяемое среднее арифметическое при большом количестве метрик не умеет замечать отклонения по отдельным показателям.

В комплексных системах оценки, включающих в себя и несколько процессов, и проектную деятельность, и качество услуг, и оценку руководителя, количество показателей часто находится в диапазоне 10-20 штук. Для среднего арифметического это слишком много. Более того, как было показано позднее, в такой ситуации не спасает и каскадирование средних. Нужен был алгоритм, который обеспечивал бы более строгую оценку.

Это и было главной сильной стороной среднего с динамическими весами. По мере отклонения метрик от своих целевых значений их вес рос, и алгоритм «откликался» на это снижением интегральной оценки.

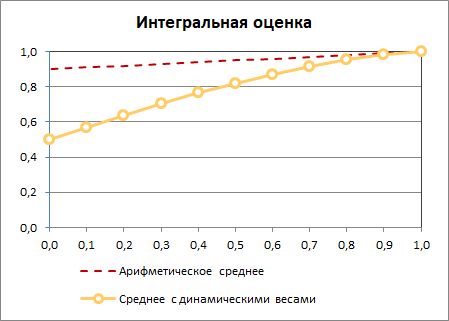
Плохой

Но разве бывают плюсы без минусов? Не обошлось без них и здесь. Вот они, представленные в порядке возрастания критичности.

Первый – алгоритм не очень хорошо учитывает «перевыполнение плана» (когда значение рейтинга метрики превышает единицу). Связано это с тем, что, согласно определению алгоритма, при R=1 вес метрики обращается в 1, независимо от её значимости. То есть перевыполнение плана не учитывает разную значимость метрик.

Второй – параметр, определяющий значимость метрик, имеет вид дробного числа между 0 и 1, в то время как для других алгоритмов приняты веса в виде натуральных чисел. Это отличие усложняет комбинирование разных алгоритмов агрегирования при автоматизации расчетов – разным алгоритмам требуются параметры разных типов.

Но все это цветочки. Третий же минус – большая ягода, причем весьма горькая. Проблема в том, что алгоритм требует большой аккуратности в выборе зависимости W( R ). Предложенная мной линейная зависимость обладает серьезным изъяном – в диапазоне R от 0 до 1 произведение RW( R ) не является монотонно возрастающей функцией. Это приводит к тому, что если одна метрика, не очень значимая, имеет значение около 0, то небольшое отклонение от 1 вниз значимой метрики может неожиданно … улучшить итоговый результат. Дело в том, что вес значимой метрики при R ≈ 1 растет быстрее падения её значения, и произведение RW( R ) при уменьшении R может увеличиться. Доставайте помидоры – я готов.

Злой

Разумеется, у этой проблемы есть решение – достаточно подобрать такую функцию W( R ), для которой произведение RW( R ) в диапазоне R от 0 до 1 будет монотонно возрастать. Желающие могут поупражняться сами – сделать это несложно. Результирующая зависимость будет иметь вид обратной пропорции или схожей по поведению функции:

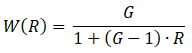
Однако такие зависимости обладают одним неприятным свойством – они довольно слабо реагируют на изменения R в диапазоне от 0.5 до 1. И только затем, при дальнейшем росте отклонения, вес метрики резко взлетает от 1 до G. Такой алгоритм долго терпит, а потом внезапно становится очень злым. Для построения системы оценки это крайне неудобно. Не решает он и первых двух перечисленных проблем. Увы.

Другой

Сказанное выше обуславливает потребность в новом подходе, и теперь у нас есть ответ в виде алгоритма, основанного на рациональной функции:

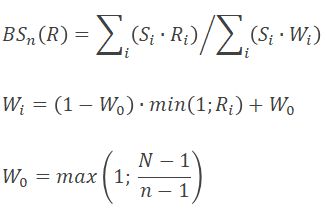
i – индекс метрики (1 ≤ i ≤ N)
Si – значимость i-той метрики (Si ≥ 1)
N – общее количество агрегируемых метрик (N ≥ 1)
n – целочисленный параметр, равный количеству метрик, при превышении которого алгоритм агрегирования начинает отклоняться от взвешенного среднего для повышения чувствительности к единичным отклонениям (n > 1).

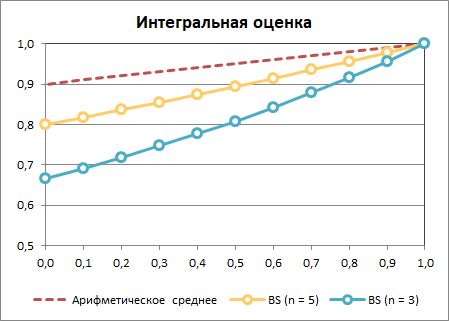
Подробное объяснение выходит за рамки – текст и так очень длинный. Но основные свойства данного алгоритма перечислить необходимо:

• При небольшом числе метрик (N ≤ n) W0 становится равным 1, и алгоритм автоматически сводится к обычному среднему арифметическому. При большем числе метрик (N > n) алгоритм начинает «ужесточаться». Разумными значениями параметра n, на наш взгляд, являются числа 3-5, то есть именно та граница, за которой среднее арифметическое требует корректировки. На картинке выше N равно 10, а n принимает значение 3 и 5.
• Все перечисленные проблемы среднего с динамическими весами в этом алгоритме устранены.

Фидбек приветствуется.

ИНТЕНСИВ С ТРЕНЕРОМ

VAP: Построение системы KPI для ИТ

Как обеспечить управление процессами, проектами, услугами, персоналом