Постановка задачи
Допустим, мы решили провести опрос пользователей. Известно, что всего их – 1 000 человек. Для простоты предположим, что мы задаём 1 вопрос (например, об удовлетворенности качеством поддержки) с ответом по пятибалльной шкале (1-5). Интересующий нас результат опроса выражается средним из полученных ответов.
Вопрос: сколько ответов пользователей необходимо получить, чтобы результаты опроса были достаточно точными (достаточно – для принятия на основании результатов опроса управленческих решений)?
Ответ первый: на основании здравого смысла (то есть предрассудков)
Я опросил несколько знакомых, как они думают, сколько голосов пользователей необходимо получить. Ответы ранжировались в диапазоне 10-50% голосов от общего количества участников опроса, наиболее часто – 10-20% (то есть в нашем примере с 1 000 пользователей нам необходимо получить 100-200 голосов).
Ответ второй: на основании математики
Статистику учил очень давно. А поскольку период полураспада знаний среднего студента составляет один семестр, знаний в моей голове практически не осталось. Пришлось повторять. Результат повторения, вкратце, таков.
Выборочное среднее отличается от среднего по генеральной совокупности, и это отличие может быть выражено с помощью доверительного интервала. Доверительный интервал представляет собой диапазон значений, в который с заданной вероятностью попадает среднее по генеральной совокупности. Для небольших выборок случайных величин, распределенных по нормальному закону, доверительный интервал может быть рассчитан при помощи распределения Стьюдента:
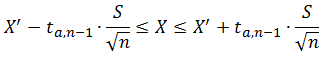
n – размер выборки (количество полученных ответов);
t(a, n-1) – коэффициент Стьюдента для вероятности 1-a;
X – среднее по генеральной совокупности («точный» средний балл);
X’ – выборочное среднее (средний балл по полученным ответам);
S – стандартное отклонение, рассчитанное по формуле:
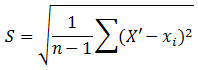
На всякий случай, всё это легко считается в MS Excel. Так в MS Excel 2010 стандартное отклонение рассчитывается функцией СТАНДОТКЛОН.В(…), доверительный интервал можно получить вызовом функции ДОВЕРИТ.СТЬЮДЕНТ(a; S; n), а коэффициент Стьюдента – функцией СТЬЮДЕНТ.ОБР.2Х(a; n-1).
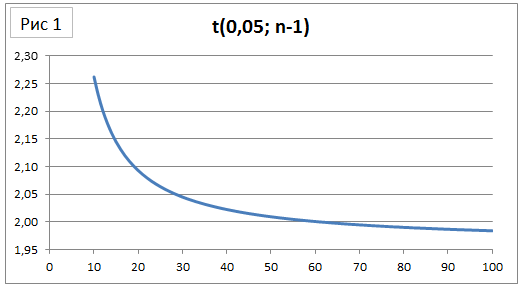
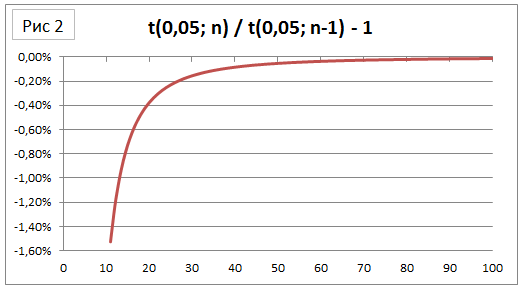
Теперь посмотрим на границы доверительного интервала повнимательнее. На рисунке 1 представлен коэффициент Стьюдента для вероятности 95% в зависимости от размера выборки. На рисунке 2 – изменение коэффициента Стьюдента при увеличении выборки на единицу. Видно, что после n=40 уменьшение коэффициента Стьюдента практически не наблюдается (при увеличении выборки на единицу изменение коэффициента Стьюдента составляет менее -0,1%). Это значит, что, увеличив размер выборки вдвое (например, получив вместо 40 ответов 80), мы сокращаем доверительный интервал всего на 30% (при условии сохранения выборочного среднего и стандартного отклонения, см. раздел про границы применимости). Не так уж и много.
Далее, для опроса по пятибалльной шкале ответы обычно укладываются в диапазон 2-5, а значит стандартное отклонение ограничено сверху примерно на уровне 1,5 (обычный диапазон значений – от 0,5 до 1,2). Таким образом, при 40 ответах точность результата составляет 0,25-0,5 балла и с дальнейшим ростом выборки (вспоминая предыдущий абзац) сокращается относительно слабо. Так, при 100 ответах получаем точность на уровне 0,15-0,3 балла, и это при том, что мы опросили в 2,5 раза больше пользователей.
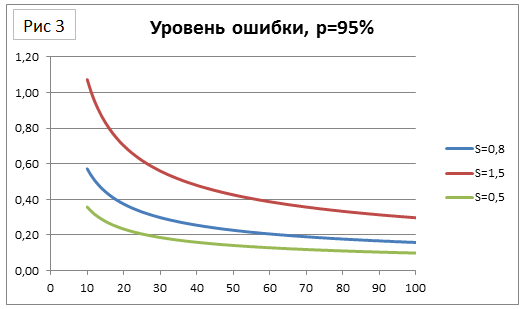
Таким образом, математика показывает, что оценка 10-20%, полученная на основании здравого смысла, завышена. При пятибалльной шкале ответов достаточно опросить порядка 40-50 пользователей. Что любопытно, это число не зависит от размера организации, то есть даже если пользователей будет 10 000, результат останется тем же: 40-50 ответов (в то время как оценка 10-20% даст выборку 1 000 – 2 000 ответов!).
Важно: увеличение точности шкалы ответов (например, не 5, а 10 баллов) в целом ведет к более высоким требованиям к размеру выборки (поскольку увеличение стандартного отклонения приводит к увеличению ошибки).
Границы применимости математического аппарата
Известный математик Давид Гильберт говорил: «Математика никогда не знает, о чем она говорит и верно ли то, о чем она говорит». И у этой шутки есть очень хорошее, глубокое объяснение, но об этом отдельно.
Нам же важно то, что математика, приведенная выше, предполагает, что ответы пользователей подчиняются нормальному распределению (то есть случайны). Не исключено, однако, что на наш вопрос о качестве поддержки сначала «набегут» отвечать наиболее недовольные и, таким образом, небольшая выборка может дать заниженную оценку. Таким образом, если пользователи «кластеризуются» по вариантам ответов (например, Вы знаете, что филиалы довольны меньше, чем головной офис из-за медленных каналов и неудобных телефонов), по 40-50 голосов необходимо получить от каждой группы пользователей. Но выявление таких групп есть путь предположений, возможны ошибки. Об этом необходимо помнить.
Выводы
С оговоркой про границы применимости математики я бы сделал следующие выводы:
- На основании здравого смысла мы склонны завышать требования к количеству ответов, необходимому для подведения итогов опросов.
- Даже небольшие выборки (40-50 ответов при 1 000+ пользователей) при не слишком сложной шкале ответов (пятибалльная шкала) могут быть достаточно точны (ошибка в 0,25-0,5 балла с вероятностью 95%), чтобы опираться на них при принятии решений.
Вообще, у меня в голове всегда сидела и сидит цифра 5%. Откуда она там взялась, я честно не помню (очень возможно, из курса в институте как раз, это был один из немногих действительно понравившихся мне предметов) 🙂
Эту же цифру мы всегда использовали, когда оценивали необходимое количество для выборки по опросам пользователей по департаментам. Оказывается за этой цифрой есть целый матаппарат
"Если б Остап узнал, что он играет такие мудреные партии и сталкивается с такой испытанной защитой,он крайне бы удивился…"